Sous différentes formes, l’engrenage est partout dans le moulin. Il en existe d’ailleurs de nombreux aspects propres à dérouter le mécanicien contemporain. Proposons nous donc une étude de cas.
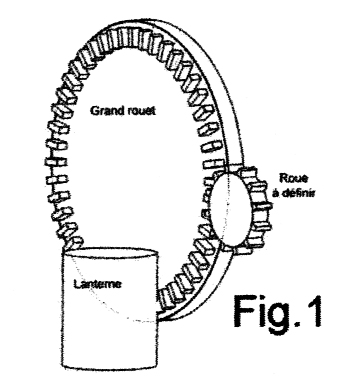
Il s’agirait, par exemple, de définir une roue entraînant une transmission auxiliaire, qui viendrait engrener sur la denture du grand rouet d’un moulin à vent. Alors, la denture du grand rouet fonctionnerait à la fois en renvoi d’angle sur la lanterne à
fuseaux, et en roue cylindrique sur celle à définir. (fig.1) Ici, nous avons une roue déjà définie, comment déduire la denture à tracer de la denture existante? Plutôt que de s’en remettre à l’intuition ou à des recettes incertaines, nous essayerons
une méthode simple (1), quoique assez peu précise.
Mise en place
Supposons au grand rouet 48 dents en forme de prisme parallélépipédique, de base 60 x 30 mm.
Diamètre de tête (extérieur) relevé 1200 mm.
Le pignon aurait 12 dents, d’où un rapport de transmission de 48 : 12 = 4. Remarquons tout de même que :
• l’intervalle (l’espace entre dents) est plus grand que l’épaisseur (2). Cette particularité favorise le pignon, toujours plus faible que la roue.
• ici les divisions proposées sont des multiples de 12, cas fréquent facile à tracer. Dans l’absolu, il vaudrait mieux choisir des nombres premiers entre eux.
• 12 est un nombre un peu faible pour un pignon mené, cas défavorable, d’où un risque de “dur” en fonctionnement.
Que dit la théorie ?
Un engrenage se comporte comme un couple de roues de friction, roulant sans glissement sur leurs cercles primitifs. Ces derniers n’appartiennent pas aux données du problème et il faut les définir.
Choisissons encore 1200mm pour la roue, nous verrons pourquoi. Alors celui du pignon sera 1200 : 4 = 300 mm.
Résumons : La roue 1 est connue (grand rouet), en particulier par son primitif et sa denture au profil C1 (d’ailleurs ici, parfaitement arbitraire). Le problème consistera donc à déterminer une courbe C2, la conjuguée de C1, appartenant à la roue 2
(le pignon)(fig.2).
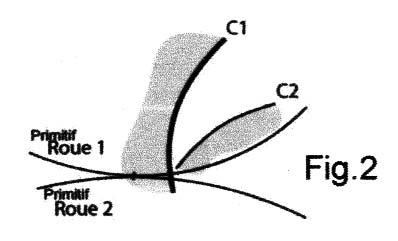
On démontre qu’en fonctionnement, ce profil C1 enveloppe une courbe C2, unique, appartenant à la roue 2. C2 est le profil recherché. On dit que C1 et C2 sont conjuguées.
Le principe consistera donc à faire rouler – virtuellement (3) – sur leurs primitifs, la roue donnée (le grand rouet : la roue) sur la roue à définir (le pignon), de façon à en déduire l’enveloppe du profil donné dans cette roue.
Tracé
Pour matérialiser le roulement sans glissement, traçons sur les primitifs une série de divisions égales notées 1,2,3,4, etc. qui se correspondent. Pratiquement, ces points s’obtiennent par report de longueurs égales, autrement dit , en assimilant les cordes aux arcs. Par conséquent, ces divisions ne seront ni trop serrées (cumul d’erreurs de report), ni trop lâches (“polygonisation” des cercles).
Sur la roue, on peut considérer que C1 enveloppait une série de courbes. Par simplicité, ce sera une file de cercles c1, c2, c3, etc. centrés en 1, 2, 3, … et tangents à C1.
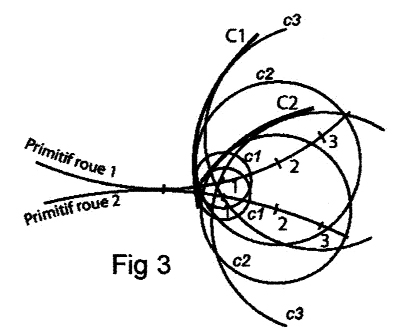
Il s’agit de transposer (même rayon, centre pris sur les divisions correspondantes) cette file de cercles sur le pignon, dont l’enveloppe sera le profil conjugué cherché. (voir fig. 3).
Ainsi, la courbe C1 est connue (ici une droite), le point 3 aussi. Dans la roue 1, chercher (par tâtonnement) un cercle c3 , de centre 3, tangent à C1 donné. Dans la roue 2, de 3 comme centre, tracer son homologue c3 (même rayon). Une fois obtenue la file de cercles de la roue 2, tracer son enveloppe C2, c’est à dire, une courbe tangente commune. C2 est le profil cherché, conjugué de C1.
La valeur du résultat dépend entièrement de la précision du tracé : opérer en vraie grandeur …
Résultat et Critique
Bien entendu, il conviendrait de développer davantage certains points d’une telle présentation dépouillée à un strict minimum. Signalons au moins que :
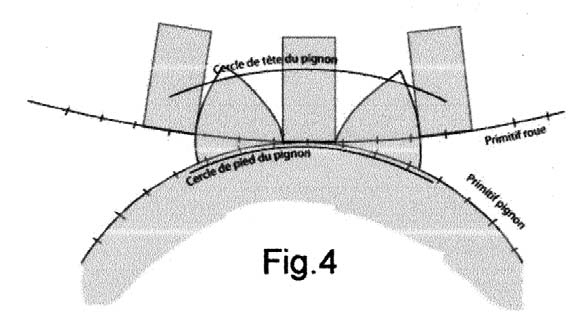
• La dent ne doit pas devenir pointue (les flancs opposés se recouper), donc fragile. Limitons son diamètre de tête à 385 mm par exemple.
• De même, prolongeons la dent (4) jusqu’à un cercle de pied laissant un espace raisonnable à fond de dent. Par exemple pour un diamètre de 280 mm.
• Le tracé suggère, il faudrait le vérifier, qu’il y aura toujours au moins une paire de dents en prise. L’engrènement serait donc toujours défini.
• Malheureusement, le contact se concentre au voisinage du cercle de tête des alluchons de la roue. On pourrait craindre une usure locale concentrée si les alluchons n ‘ é t a i e n t nombreux.
• Ce pied de dent donne des rayons de courbure à peu près nuls, ce qu’il vaut mieux éviter: La dent souffrirait considérablement à cet endroit. Par ailleurs, si l’on avait défini le primitif au milieu du profil donné, comme on serait tenté de le faire par idée de “symétrie”, il y aurait eu interférence(5).
• L’usage voulait que l’on donne un jeu de fonctionnement d’un ordre de grandeur de 10 à 15% de l’épaisseur de la dent. Il ne doit pas s’obtenir pas une augmentation de l’entre axes au montage, mais par le tracé d’une courbe parallèle au profil exact.
En tout cas ces opérations n’auraient de sens qu’en s’assurant sérieusement au préalable des déformations acquises, rigidité générale, jeux et position effectifs des assemblages. Rien ne remplace le bon sens…
Jean Wehrlé – Article paru dans le Monde des Moulins – N°13 – juillet 2005



0 commentaire